single layer and multilayer feed forward networks

A feedforward neural network is an artificial neural network wherein connections between the units do not form a cycle. As such, it is different from recurrent neural networks.

The feedforward neural network was the first and simplest type of artificial neural network devised. In this network, the information moves in only one direction, forward, from the input nodes, through the hidden nodes (if any) and to the output nodes. There are no cycles or loops in the network.

The simplest kind of neural network is a single-layer perceptron network, which consists of a single layer of output nodes; the inputs are fed directly to the outputs via a series of weights. In this way it can be considered the simplest kind of feed-forward network. The sum of the products of the weights and the inputs is calculated in each node, and if the value is above some threshold (typically 0) the neuron fires and takes the activated value (typically 1); otherwise it takes the deactivated value (typically -1). Neurons with this kind of activation function are also called artificial neurons or linear threshold units. In the literature the term perceptron often refers to networks consisting of just one of these units. A similar neuron was described by Warren McCulloch and Walter Pitts in the 1940s.

Multilayer Feedforward Neural Networks

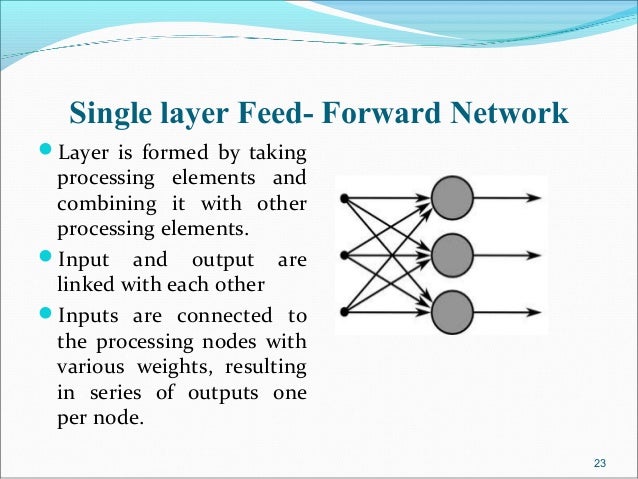
A multilayer feedforward neural network is an interconnection of perceptrons in which data and calculations flow in a single direction, from the input data to the outputs.  The number of layers in a neural network is the number of layers of perceptrons.  The simplest neural network is one with a single input layer and an output layer of perceptrons.  The network in Figure 13-7 illustrates this type of network.  Technically, this is referred to as a one-layer feedforward network with two outputs because the output layer is the only layer with an activation calculation.

Figure 13- 7:  A Single-Layer Feedforward Neural Net

In this single-layer feedforward neural network, the network’s inputs are directly connected to the output layer perceptrons, Z₁ and Z₂. 

The output perceptrons use activation functions, g₁ and g₂, to produce the outputs Y₁ and Y₂.

Since

 ,

,

and

.

When the activation functions g₁ and g₂ are identity activation functions, the single-layer neural net is equivalent to a linear regression model.  Similarly, if g₁ and g₂are logistic activation functions, then the single-layer neural net is equivalent to logistic regression.  Because of this correspondence between single-layer neural networks and linear and logistic regression, single-layer neural networks are rarely used in place of linear and logistic regression.

The next most complicated neural network is one with two layers.  This extra layer is referred to as a hidden layer.  In general there is no restriction on the number of hidden layers.  However, it has been shown mathematically that a two-layer neural network

can accurately reproduce any differentiable function, provided the number of perceptrons in the hidden layer is unlimited.

However, increasing the number of perceptrons increases the number of weights that must be estimated in the network, which in turn increases the execution time for the network.  Instead of increasing the number of perceptrons in the hidden layers to improve accuracy, it is sometimes better to add additional hidden layers, which typically reduce both the total number of network weights and the computational time.  However, in practice, it is uncommon to see neural networks with more than two or three hidden layers.